Hàm gia tốc (Easing functions) là một công cụ vô cùng hữu ích cho các họa sỹ diễn xuất animator. Chúng rất tiện dụng khi chúng ta muốn tạo ra một chuyển động với cái nhìn mới mẻ, bóng bẩy hơn, và rất dễ sử dụng trong các đoạn code.
Bản chất vấn đề là bạn có một điểm khởi đầu A và điểm kết thúc B, và bạn muốn một cái gì đó di chuyển từ A đến B dọc theo một đường (không nhất thiết là đường thẳng) để kết nối cả hai điểm trên.
Tuy nhiên, đường đi giữa các điểm không phải là điều duy nhất cần phải xem xét mà còn phải xét đến cách đối tượng sẽ đi qua con đường này, tốc độ nó sẽ di chuyển ở mỗi điểm, và nó sẽ tăng tốc như thế nào,…
Những gì chúng ta đang tìm kiếm ở đây là tham số “tốc độ” chuẩn của đường đi, tương ứng một hàm f(t) trả về một điểm trong không gian dọc theo đường đi. Các hàm số được thiết lập tại f(t=0) cho chúng ta điểm khởi đầu và f (t=1) cho chúng ta điểm kết thúc. Ngoài ra, đối với các giá trị khoảng cách t đều nhau trong khoảng thời gian [0,1], chúng ta có được các điểm đều nhau trên đường đi.
Tham số tốc độ đơn vị của các đường cong không nhỏ, nhưng đối với một đường thẳng bằng cách sử dụng nội suy tuyến tính, nó gần như là bất biến và chuẩn hóa tại một tốc độ nhất định.
Đây là hàm gia tốc đi. Hàm gia tốc e(t) lấy giá trị đầu vào t, từ 0 đến 1, và trả về một giá trị mới, không nhất thiết là 0 đến 1 (để bù cho việc vượt tốc). Các ràng buộc duy nhất là e(0)=0 và e(1)=1. Giá trị trả lại bởi hàm gia tốc chính là vị trí hiện tại dọc theo đường đi.
Về mặt toán học, nếu đường đi được cho bởi hàm f(t) và hàm gia tốc e(t), chúng ta sẽ sử dụng f(e(t)) trong đoạn code cần diễn xuất.
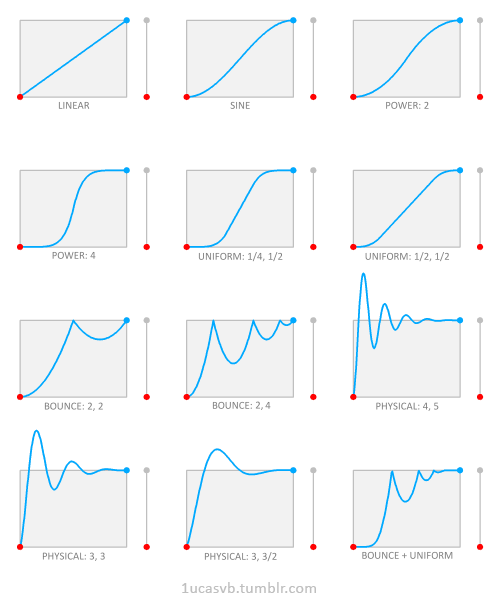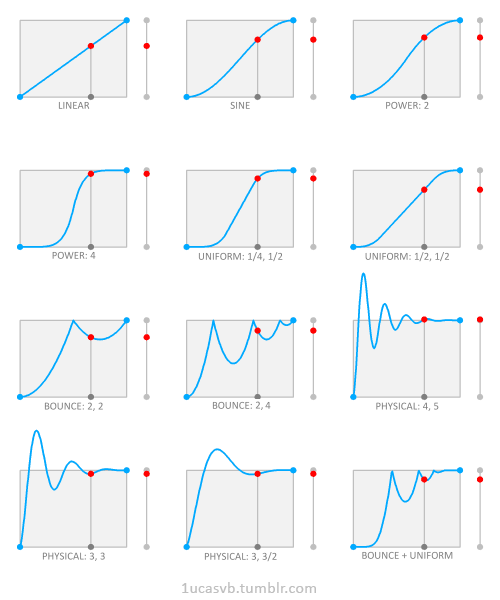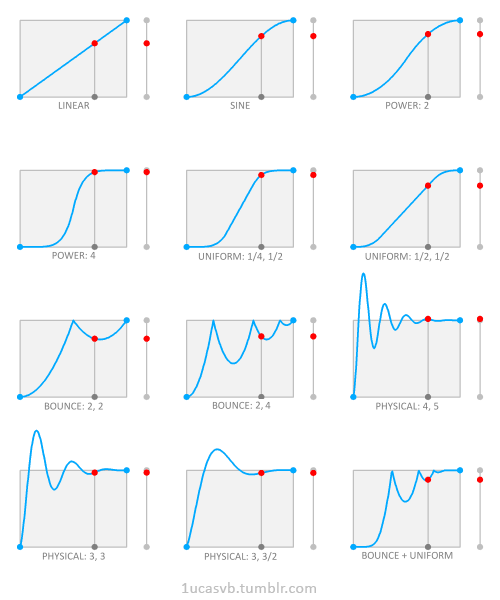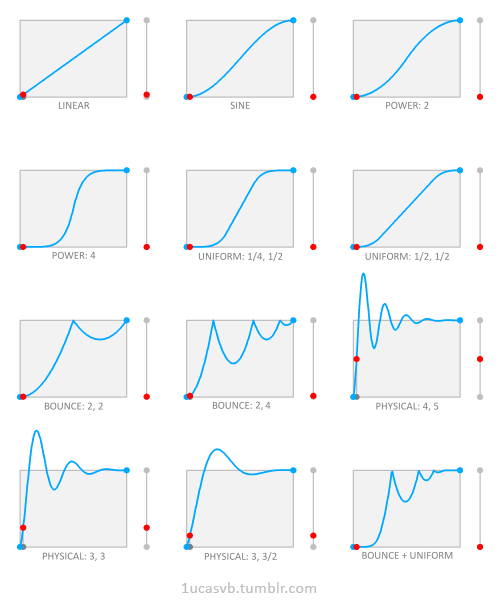
Theo đó, bạn sẽ thấy kết quả của việc sử dụng một số hàm gia tốc khác nhau trên một đường đi tuyến tính đơn giản.
Giá trị trục hoành của mỗi đồ thị là tham số thời gian t, và giá trị trục tung là giá trị trả về e(t). Hộp phân cách khoảng từ [0,1] theo cả hai hướng.
Phần bên phải mỗi đồ thị là chuyển động bạn nhận được từ hàm gia tốc. Bạn có thể thấy rằng ngay cả những biến đổi nhỏ nhất từ đường thẳng siêu vụng (trên cùng bên trái) đã được làm đẹp hơn rất nhiều .
Các hàm được trình bày trên đây đều được hiệu chỉnh, và là một phần của thư viện diễn xuất cá nhân. Linear, power và sine là những hàm cơ bản có thể thấy ở mọi nơi.
Hầu hết các thư viện đều có “elastic” và “bounce”,… nhưng luôn có đường cong Bézier cố định hoặc đường định tuyến (polynomial approximation). Điều đó không linh hoạt khi bạn muốn chỉnh chúng theo nhu cầu, nên cần phải tạo những hàm riêng.
Dĩ nhiên, các hàm này chưa đáp ứng được tính thương mại, do chưa tối ưu hóa được thời gian thực hiện, nhưng đó không phải là vấn đề cần quan tâm ở đây.
Bạn sẽ nói rằng sao không tách riêng ease-in và ease-out?! Điều này gần như không cần. Tôi chưa thấy ai sử dụng “elastic/bounce ease in” cả.
Dù bất kỳ trường hợp nào, việc tạo ra các hàm hỗn hợp từ những điều này cũng rất dễ dàng, chỉ cần reverse một nửa khoảng thời gian, và loại trừ hàm số từ giá trị 1 cho các phần ease-in.
POWER
Có 3 loại: quad(tratic), cubic và quart(ic). Tôi quyết định gom chúng vào cùng một nhóm, vì chúng có cùng cấu trúc, ngoại trừ sử dụng các power khác nhau.
Ý tưởng là sử dụng một biến thể của tp và sự phản chiếu của nó để tạo ra các bit ease-in và ease-out.
Cụ thể, bạn có (2t)p/2 cho t trong [0,0.5] và 1-(2 (1-x))p/2 (clarity không mở rộng) cho t in (0.5,1). Các giá trị p>0 được xử lý tốt trong một đơn vị thời.
SINE
Đơn giản là sin(t • π / 2) 2. Bạn có thể dễ dàng loại bỏ power đó bằng cách sử dụng đồng nhất thức quen thuộc, và dễ nhìn hơn cách này.
BOUNCE
Bounce dựa trên chuyển động vật lý của parabol. Nó được điều chỉnh bởi hai tham số: power phân rã và số lần chạm đất. Điều này có nghĩa là bạn có thể thiết lập một cách chính xác, số lần bạn muốn nó bounce xung quanh, và bạn có thể điều chỉnh mức năng lượng sau mỗi bounce.
Tôi thường tránh sử dụng phân rã mũ theo cách riêng của nó bởi vì nó không đạt được chính xác vào lúc cuối, mà thường là mong muốn hơn so với tỷ lệ phân rã vật lý chính xác. Vì vậy, tôi có xu hướng sử dụng một yếu tố (1-t)p để phân rã nói chung.
PHYSICAL
Hầu hết các thư viện bao gồm “elastic” và “back” nhưng chúng không thể hiện chuyển động vật lý chính xác, và không thể tinh chỉnh nhiều.
Hàm gia tốc “physical” thay thế cho cả hai bằng một giải pháp cho dao động điều hòa giảm chấn, ở đó bạn có thể tự thiết lập tốc độ phân rã và tần số dao động. Điều này giúp bạn có thể điều khiển chính xác chuyển động theo ý bạn muốn. Tỷ lệ phân rã mũ cũng được thay thế bằng biểu thức p(1-t)p.
Sử dụng các tần số như 1 hoặc 0.5 cho phép bạn thay thế cho “back” easing trong các thư viện khác, với lợi ích của việc điều chỉnh. Không hẳn ½ tần suất theo hướng xấu, mà nhờ chức năng phân rã chúng vẫn kết thúc ở 1 mà không có vấn đề gì.
UNIFORM
Trong đa số trường hợp, “uniform” thực hiện chuyển động “gần như tuyến tính”, với một tốc độ ổn định. Vấn đề lớn nhất với nội suy tuyến tính là những điểm kết thúc. Việc có một vật thể tĩnh và đột ngột di chuyển có vẻ nghịch lý và không thực tế.
“Uniform” easing có thể giữ cân bằng cho cả hai điều: bạn có thể điều chỉnh bao nhiêu đường đi sẽ tuyến tính, và phần còn lại sẽ được sử dụng tăng tốc / giảm tốc. Bạn cũng có thể điều chỉnh tốc độ tăng tốc / giảm tốc.
Do tính chất gần như tuyến tính của nó, nó hoạt động đặc biệt tốt với các hàm gia tốc khác.







